D2
Администратор
- Регистрация
- 19 Фев 2025
- Сообщения
- 4,380
- Реакции
- 0
Автор n0_mad
Статья написана для Конкурса статей #10
Вступление.

Шрифт Брайля, названный в честь так же потерявшего зрение вследствие инфекции Луи Брайля, помогает слепым получать информацию, а именно текстовую посредством осязательной-тактильной функции. В шрифте ничего сложного и это такой же алфавит, где каждая буква имеет свое наполнение проколотыми и нетронутыми точками в клетках, размером 2 столбца и 3 строчки, а так же соответсвующее значение. Однако, что, если я предложу рассмотреть, придуманный в далеком 1824 году, шрифт для незрячих в области шифрования данных и криптографии для зрячих(никакой дискриминации)? Ироничное предыдущее предложение.
Давайте чуть сбавим градус напряжения в гонке за главными призами, всеобщего недовольства первым упоминанием XOR и метода с блокнотом в рамках конкурса и рассмотрим теорию перед попыткой апгрейдов и практического применения.
Конкурс, да ещё и фонд помноженный на 2, заставляют палить постоянных и не очень авторов из всех орудий.
Введение.
Итак, для самых юных читателей или тех, кто только погружается в область криптографии, будет дан простой аналог, чтобы можно было понять о чём речь.
Допустим, что ваш родной язык - русский, вы приходите на переговоры. Ваши оппоненты говорят на арабском, которого вы не знаете. В итоге это выглядит очень примерно как зашифрованное общение, так как в данном кейсе, “арабский язык” - ключ для дешифровки того, о чём речь между двумя собеседниками. Учитывая, что арабский язык ещё и не очень-то простой в изучении, то и шифр “взломать” не очень просто, но условные "ключи" в виде словаря всё же слили когда-то в паблик
Поставлена задача как раз и сделать алгоритм шифрования обоснованным логически, удобным, вычислительно быстровыполняемым(для скорости передачи данных), а самое важное - безопасным для использования. Я соглашусь сразу с любой критикой. Да, конечно, можно придумать хоть иероглифы и наскальную живопись использовать, но только тогда как это логически обосновать, сделать хаотичным, программно описать вычисления, чтобы генерация была случайной, но структурированной?
- Я предлагаю разобраться, а сам алгоритм найдёт того, кому он может прийтись по вкусу.
Теория и планирование.
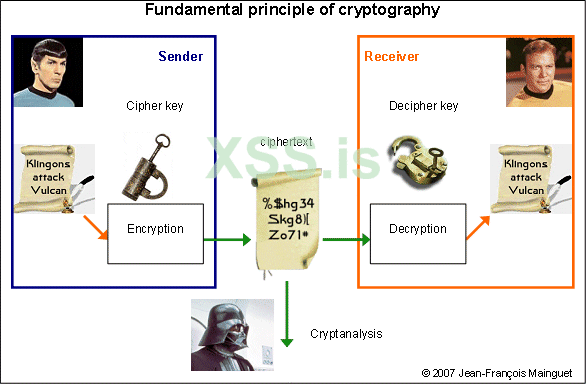
Основное в шифровании это то, чтобы тот, кто не должен знать сообщение - всё же его и не узнал.
То есть нам нужно, чтобы виды атак и способы расшифровки сводились к минимуму, а следовательно криптоанализ, частотный анализ и другие подходы к шифру должны быть защищены.
Таким образом, получается, что у нас есть “план шифра”:
Создание значений, соответсвуя Брайлю.
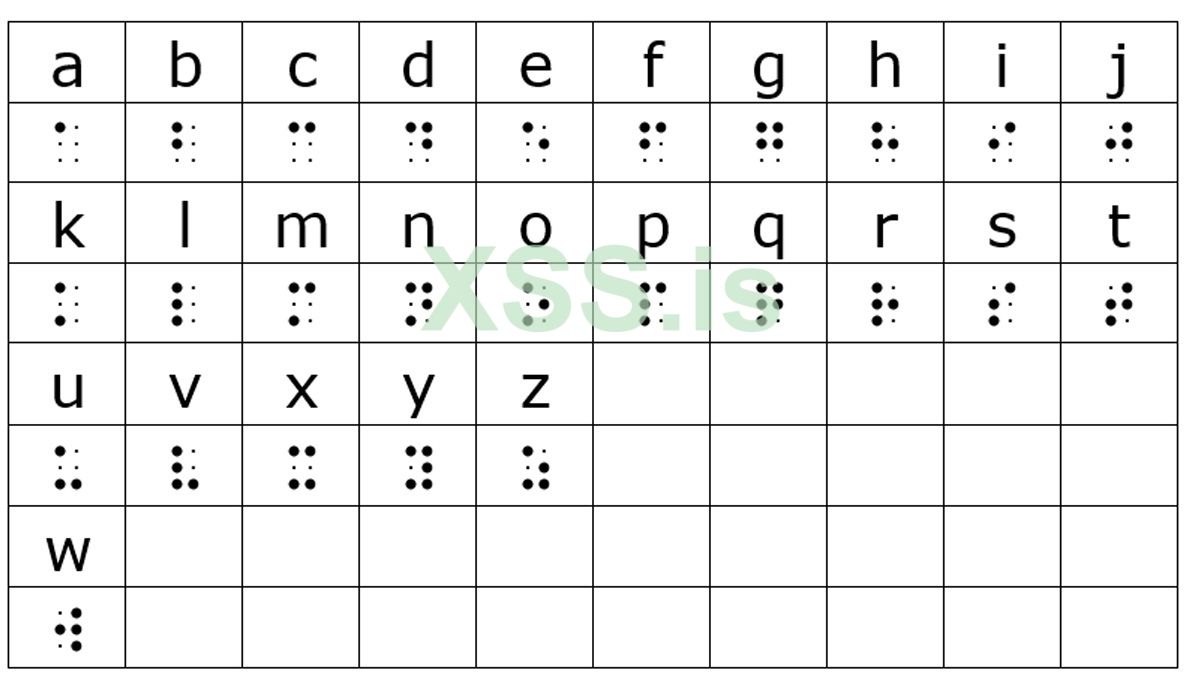
Как мы видим на картинке, на которой изображен шрифт Брайля и алфавит, нам вполне подходит структура для того, чтобы создать фундамент шифрования, соотнося точки “прокола” с бинарным кодом (1 и 0).
Каждая точка - бинарное значение, каждая “ячейка”, т.е. пустая точка - 6-ти битное число. Всего мы сможем закодировать 64 символа, так как используется клетка 2 х 3.
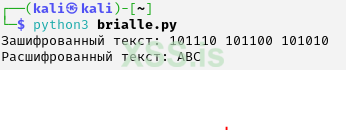
Для примера возьмём букву “A”. которая выглядит в шрифте Брайля так:

Как мы видим, заполнена только первая точка, представим это как “100000”, следовательно бинарное значение(b) для буквы “А” = 32.
В случае с буквой “Б”, значение b = 48(110000), “В” - b = 36(100100) и так далее.
В предложенном алгоритме, для шифрования и получения ключа будут выполнены XOR-операции, что поспособствует получению результата.
Предположим, что мы хотим зашифровать “АБВ”(ABC в латин.), таким образом у нас получится результат вычислений отдельных букв “А”, “Б и “В” и итогове значение “110100”, которое является ключом, где b = 52.
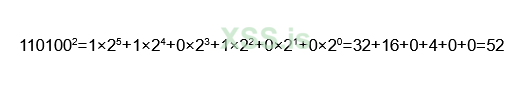
Наглядные вычисления:
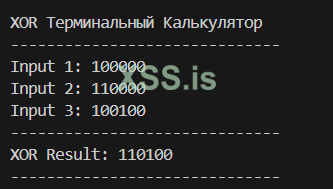
Результат на лицо - получение ключа, благодаря XOR.
Как тут вообще работает XOR-операционка?
Так как целью является вычисления между двоичным кодом и соответствующим битом, то мы, преобразовав каждую букву в бинарный вид, применяем XOR ключ.
Небольшим бонусом ещё идёт то, что каждыми данными операциями мы сравниваем каждый бит независимо друг от друга. Оба бита равны - результат 0, оба разые - результат 1.
Для "А" это будет выглядеть так:
"А" = "100000".
"Ключ" = "110100"
Последующая передача полученного зашифрованного текста(в данном случае это именно результат XOR-операций) получателю будет представлен в таком виде: "010100"
Следовательно, для обратного эффекта, то бишь расшифровки, получатель должен знать ключ и выполнить аналогичный процесс, применив XOR ключ и пройдя процесс дешифровки.
В результате получив бинарные значения, соответствующие буквам “А”, “Б” и “В”, а двоичный код, преобразуя согласно заданным в шифре значениям из таблицы Брайля.
- Бонус XOR-calculator прямо в терминале для самых ленивых:
Python: Скопировать в буфер обмена
Увеличим количество "ячеек".
За счёт увеличения количества ячеек, которые заполняются точками, например до 2, возможно и повысить безопасность самого шифра, ведь 2^12 = 4096(в десятичной системе) лучше, чем 64, не так ли?
В нашем случае, за счёт того что возможно заполняемых точек уже не 6, а 12. В купе с генерацией случайных событий, вполне реально усложнить задачу по вычислению что, где и когда.
Например, мы взяли две ячейки, в которой заполнена только первая точка, а остальные пусты.
В таком случае мы получим, что для буквы “А” предполагаются 2 ячейки(4 x 6):
Для примера вычислений в случае шифрования мы возьмём 2 буквы - “А” и “Б” и представим их в виде строки “АБ” и используем маскировку в виде случайных чисел для XOR-операций.
Тогда наши операции будут выглядеть следующим образом:
Для “А”.
Первая ячейка: 100000 XOR 011011(random) = 111011
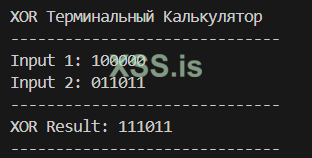
Вторая ячейка: 000000 XOR 101010(random) = 101010
Для “Б”.
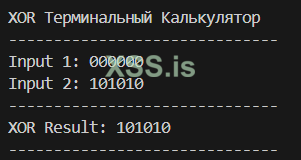
Первая ячейка: 110000 XOR 011011(random) = 101011
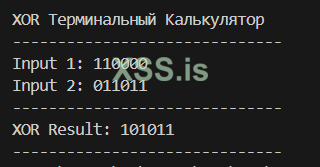
Вторая ячейка: 000000 XOR 101010(random) = 101010
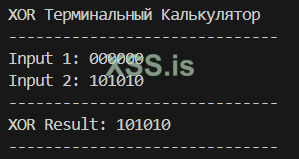
В конечном результате операций мы получим зашифрованное сообщение: 111011 101010 101011 101010
- Я бы выделил из плюсов тот факт, что метод перебора будет значительно затруднён, особенно за счёт увеличения с 64 до 4096 возможных значений.
Настало время двигать.
Дополнительный вариант, который я предлагаю использовать для того, чтобы граждане в чёрных шляпах не стали докучать нам частотным анализом - двигать точки после XOR-операции.
- Что это ещё такое, возмущённо спросите вы?
Давайте смиримся с тем, что в шифровании нужен баланс хаотичности и порядка, а такой финт даёт нам возможность усложнить анализ методом подбора, так как предсказуемость нивелируется.
Рассмотрим на примере:
У нас есть буква “А” и как мы помним, её значение “100000”, логично предположить, что она встречается чаще в словах, чем буква “Ю”, например, следовательно её частота повторений будет больше, а как следствие вычисление значения “А” может быть проще.
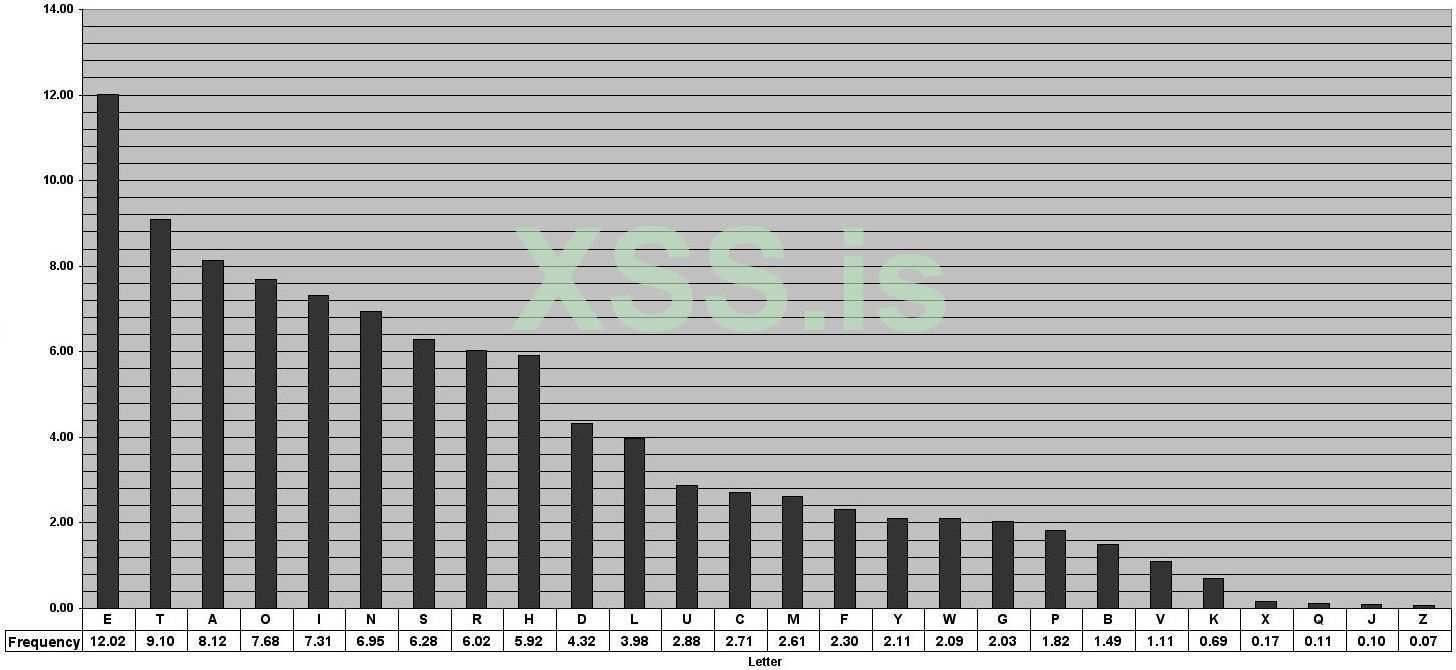
Зададим наш ключ так же, как “110100”, соответственно операция XOR с значением буквы “А” предоставит нам результат шифрования = “010100”.
При этом, посчитав количество единц в ключе, происходит сдвиг. Ключ = “110100” - сдвиг происходит на количество “заполненных точек”, на 3 точки влево(учитываем ещё особенность использвания шрифта Брайля в целом, смотрим тут - link).
Из исходного представления в “100000” мы получаем представление со сдвигом в виде “000011” дл буквы “А”. Готово, мы немного усложнили жизнь криптоаналитикам.
Мультизадачно комбинируем методы.
Ну, а теперь время объединить одно с другим, чтобы можно было ещё чуть более спокойно спать, проводя мониторинг в половину открытого глаза. Честно, постараюсь быть краток.
Вернёмся к нашей первой букве алфавита - “А” и сразу же представим её преобразование в виде 2 ячеек, расширив последние 2 бита 2-й ячейки до 6 бит, то бишь значения будет “100000 000001” (получилось даже ассиметричненько).
Возьмём наш ключ “110100” и применив к каждой ячейке XOR, мы получаем результат:
Ячейка1 = “010100”.

Ячейка2 = “110101”.
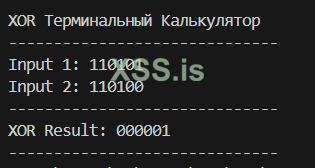
Согласно заданному методу сдвигов, мы должны при этом сместить значения точек каждой ячейки влево(кто из другого полушария - вправо ) и получить сдвиг
) и получить сдвиг по фазе после всего прочитанного текста на те самые 3 единицы. Результат нас тогда ожидает в виде “100010 101110”. Сложно.
Играемся с Python.
Настал момент истины, проверим нашу теорию технически, а то было много слов и мало дела(кроме придумывания концепции и вычислений).
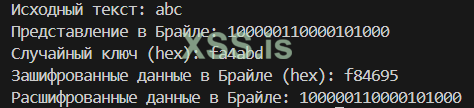
1. Мы создаём небольшой скрипт, чтобы посмотреть каким же образом наши ключи могут создаваться “случайно”, а так же как будут шифроваться и расшифровываться наши сообщения.
Код создан для наглядности процесса, но и я не самый великий Python Dev, так что используем, смотря на то как у нас что маскируется и демаскируется:
Python: Скопировать в буфер обмена
2. Сразу же заодно перейдём к тому, чтобы комбинировать методы:
Python: Скопировать в буфер обмена
Задача стояла не самая простая, для наглядности я не стал вводить и задавать специальные символы и какие-то подобные дполнительные значения, поэтому любой апгрейд на ваше усмотрение будет принят именно как апгрейд, а не критика меня как немного ленивого программиста :t
Подведём итоги.
Что ж, я очень надеюсь, что я смог обоснованно привнести задатки возможной концепции шифрования, веря, что кому-то это будет интересно.
Некоторые хотят иметь собственные методы шифрования и передачи данных, исходя из потребностей, вот и деливери оф креатив с использованием Брайля подъехал. Это лишь одна идея в зародыше из множества возможных, без реализации безопасного обмена ключами. Учитывая, что математика очень важна в самой методологии, некоторые принципы и столпы шифрования требуют гораздо больше знаний в области прикладной математики, вовзведённого аналитического подхода, программно-вычислительных возможностей и мозгов, чем есть у автора. Однако, все комментарии и желания совместных доработок - most welcome!
Всем мира в наступившем году и до новых встреч!
Статья написана для Конкурса статей #10
Вступление.
Шрифт Брайля, названный в честь так же потерявшего зрение вследствие инфекции Луи Брайля, помогает слепым получать информацию, а именно текстовую посредством осязательной-тактильной функции. В шрифте ничего сложного и это такой же алфавит, где каждая буква имеет свое наполнение проколотыми и нетронутыми точками в клетках, размером 2 столбца и 3 строчки, а так же соответсвующее значение. Однако, что, если я предложу рассмотреть, придуманный в далеком 1824 году, шрифт для незрячих в области шифрования данных и криптографии для зрячих(никакой дискриминации)? Ироничное предыдущее предложение.
Давайте чуть сбавим градус напряжения в гонке за главными призами, всеобщего недовольства первым упоминанием XOR и метода с блокнотом в рамках конкурса и рассмотрим теорию перед попыткой апгрейдов и практического применения.
Конкурс, да ещё и фонд помноженный на 2, заставляют палить постоянных и не очень авторов из всех орудий.
Введение.
Итак, для самых юных читателей или тех, кто только погружается в область криптографии, будет дан простой аналог, чтобы можно было понять о чём речь.
Допустим, что ваш родной язык - русский, вы приходите на переговоры. Ваши оппоненты говорят на арабском, которого вы не знаете. В итоге это выглядит очень примерно как зашифрованное общение, так как в данном кейсе, “арабский язык” - ключ для дешифровки того, о чём речь между двумя собеседниками. Учитывая, что арабский язык ещё и не очень-то простой в изучении, то и шифр “взломать” не очень просто, но условные "ключи" в виде словаря всё же слили когда-то в паблик
Поставлена задача как раз и сделать алгоритм шифрования обоснованным логически, удобным, вычислительно быстровыполняемым(для скорости передачи данных), а самое важное - безопасным для использования. Я соглашусь сразу с любой критикой. Да, конечно, можно придумать хоть иероглифы и наскальную живопись использовать, но только тогда как это логически обосновать, сделать хаотичным, программно описать вычисления, чтобы генерация была случайной, но структурированной?
- Я предлагаю разобраться, а сам алгоритм найдёт того, кому он может прийтись по вкусу.
Теория и планирование.
Основное в шифровании это то, чтобы тот, кто не должен знать сообщение - всё же его и не узнал.
То есть нам нужно, чтобы виды атак и способы расшифровки сводились к минимуму, а следовательно криптоанализ, частотный анализ и другие подходы к шифру должны быть защищены.
Таким образом, получается, что у нас есть “план шифра”:
- Нам необходимо преобразовать символы в значения, которые соответствуют шрифту Брайля.
- Использовать те самые злополучные XOR-операции для вычислений и шифрования. (Отдельное упоминание в данной статье Яшечке с его бесплатной раздачей вполне сносной книги, которую порекомендую всем начинающим, так как я сразу вспомнил где же это недавно мелькало в моей памяти)
- Дополнительные способы усложнения алгоритма:
3.1. Увеличение количества ячеек(2) для обозначение 1 символа. 4 х 6 клеток.
3.2. Применение сдвигов символов для усложнения частотного анализа.
3.3. Комбинирование методов. - Программная реализация на Python.
4.1. Пробы рандомизации ключей и значений с целью шифрования с помощью XOR.
4.2. Пробы представления Брайлевых значений с шифрованием с помощью XOR операций и дешифровкой, а так же комбинации методов шифрования.
Создание значений, соответсвуя Брайлю.
Как мы видим на картинке, на которой изображен шрифт Брайля и алфавит, нам вполне подходит структура для того, чтобы создать фундамент шифрования, соотнося точки “прокола” с бинарным кодом (1 и 0).
Каждая точка - бинарное значение, каждая “ячейка”, т.е. пустая точка - 6-ти битное число. Всего мы сможем закодировать 64 символа, так как используется клетка 2 х 3.
Для примера возьмём букву “A”. которая выглядит в шрифте Брайля так:
Как мы видим, заполнена только первая точка, представим это как “100000”, следовательно бинарное значение(b) для буквы “А” = 32.
В случае с буквой “Б”, значение b = 48(110000), “В” - b = 36(100100) и так далее.
В предложенном алгоритме, для шифрования и получения ключа будут выполнены XOR-операции, что поспособствует получению результата.
Предположим, что мы хотим зашифровать “АБВ”(ABC в латин.), таким образом у нас получится результат вычислений отдельных букв “А”, “Б и “В” и итогове значение “110100”, которое является ключом, где b = 52.
Наглядные вычисления:
Результат на лицо - получение ключа, благодаря XOR.
Как тут вообще работает XOR-операционка?
Так как целью является вычисления между двоичным кодом и соответствующим битом, то мы, преобразовав каждую букву в бинарный вид, применяем XOR ключ.
Небольшим бонусом ещё идёт то, что каждыми данными операциями мы сравниваем каждый бит независимо друг от друга. Оба бита равны - результат 0, оба разые - результат 1.
Для "А" это будет выглядеть так:
"А" = "100000".
"Ключ" = "110100"
| 1 | XOR | 1 | 0 |
| 0 | XOR | 1 | 1 |
| 0 | XOR | 0 | 0 |
| 0 | XOR | 1 | 1 |
| 0 | XOR | 0 | 0 |
| 0 | XOR | 0 | 0 |
Следовательно, для обратного эффекта, то бишь расшифровки, получатель должен знать ключ и выполнить аналогичный процесс, применив XOR ключ и пройдя процесс дешифровки.
В результате получив бинарные значения, соответствующие буквам “А”, “Б” и “В”, а двоичный код, преобразуя согласно заданным в шифре значениям из таблицы Брайля.
- Бонус XOR-calculator прямо в терминале для самых ленивых:
Python: Скопировать в буфер обмена
Код:
def xor_visualization(binary_values):
print("\nXOR Терминальный Калькулятор")
print("-" * 30)
###значения
for i, value in enumerate(binary_values):
print(f"Input {i + 1}: {value}")
###XOR для заданных значений
xor_result = int(binary_values[0], 2)
for value in binary_values[1:]:
xor_result ^= int(value, 2)
###форматирование в 6 bit
result_bin = f"{xor_result:06b}"
#Вывод результата
print("-" * 30)
print(f"XOR Result: {result_bin}")
print("-" * 30)
return result_bin
###взаимодействие
def main():
print("Добро пожаловать в XOR Терминальный Калькулятор!")
binary_values = []
while True:
value = input("Введите 6-битное бинарное число (или нажмите Enter для завершения): ")
if not value:
break
if len(value) == 6 and all(bit in "01" for bit in value):
binary_values.append(value)
else:
print("Пожалуйста, введите корректное 6-битное бинарное число.")
if len(binary_values) < 2:
print("Вам нужно ввести хотя бы два числа для выполнения XOR.")
else:
xor_visualization(binary_values)
###запуск
if __name__ == "__main__":
main()Увеличим количество "ячеек".
За счёт увеличения количества ячеек, которые заполняются точками, например до 2, возможно и повысить безопасность самого шифра, ведь 2^12 = 4096(в десятичной системе) лучше, чем 64, не так ли?
В нашем случае, за счёт того что возможно заполняемых точек уже не 6, а 12. В купе с генерацией случайных событий, вполне реально усложнить задачу по вычислению что, где и когда.
Например, мы взяли две ячейки, в которой заполнена только первая точка, а остальные пусты.
В таком случае мы получим, что для буквы “А” предполагаются 2 ячейки(4 x 6):
- Ячейка 1 (с заполненной точкой) = “100000”
- Ячейка 2 (пустая) = “000000”
Для примера вычислений в случае шифрования мы возьмём 2 буквы - “А” и “Б” и представим их в виде строки “АБ” и используем маскировку в виде случайных чисел для XOR-операций.
Тогда наши операции будут выглядеть следующим образом:
Для “А”.
Первая ячейка: 100000 XOR 011011(random) = 111011
Вторая ячейка: 000000 XOR 101010(random) = 101010
Для “Б”.
Первая ячейка: 110000 XOR 011011(random) = 101011
Вторая ячейка: 000000 XOR 101010(random) = 101010
В конечном результате операций мы получим зашифрованное сообщение: 111011 101010 101011 101010
- Я бы выделил из плюсов тот факт, что метод перебора будет значительно затруднён, особенно за счёт увеличения с 64 до 4096 возможных значений.
Настало время двигать.
Дополнительный вариант, который я предлагаю использовать для того, чтобы граждане в чёрных шляпах не стали докучать нам частотным анализом - двигать точки после XOR-операции.
- Что это ещё такое, возмущённо спросите вы?
Давайте смиримся с тем, что в шифровании нужен баланс хаотичности и порядка, а такой финт даёт нам возможность усложнить анализ методом подбора, так как предсказуемость нивелируется.
Рассмотрим на примере:
У нас есть буква “А” и как мы помним, её значение “100000”, логично предположить, что она встречается чаще в словах, чем буква “Ю”, например, следовательно её частота повторений будет больше, а как следствие вычисление значения “А” может быть проще.
Зададим наш ключ так же, как “110100”, соответственно операция XOR с значением буквы “А” предоставит нам результат шифрования = “010100”.
При этом, посчитав количество единц в ключе, происходит сдвиг. Ключ = “110100” - сдвиг происходит на количество “заполненных точек”, на 3 точки влево(учитываем ещё особенность использвания шрифта Брайля в целом, смотрим тут - link).
Из исходного представления в “100000” мы получаем представление со сдвигом в виде “000011” дл буквы “А”. Готово, мы немного усложнили жизнь криптоаналитикам.
Мультизадачно комбинируем методы.
Ну, а теперь время объединить одно с другим, чтобы можно было ещё чуть более спокойно спать, проводя мониторинг в половину открытого глаза. Честно, постараюсь быть краток.
Вернёмся к нашей первой букве алфавита - “А” и сразу же представим её преобразование в виде 2 ячеек, расширив последние 2 бита 2-й ячейки до 6 бит, то бишь значения будет “100000 000001” (получилось даже ассиметричненько).
Возьмём наш ключ “110100” и применив к каждой ячейке XOR, мы получаем результат:
Ячейка1 = “010100”.
Ячейка2 = “110101”.
Согласно заданному методу сдвигов, мы должны при этом сместить значения точек каждой ячейки влево(кто из другого полушария - вправо
Играемся с Python.
Настал момент истины, проверим нашу теорию технически, а то было много слов и мало дела(кроме придумывания концепции и вычислений).
1. Мы создаём небольшой скрипт, чтобы посмотреть каким же образом наши ключи могут создаваться “случайно”, а так же как будут шифроваться и расшифровываться наши сообщения.
Код создан для наглядности процесса, но и я не самый великий Python Dev, так что используем, смотря на то как у нас что маскируется и демаскируется:
Python: Скопировать в буфер обмена
Код:
import os
###шрифт Брайля исходники
BRAILLE_TABLE = {
'a': '100000',
'b': '110000',
'c': '101000',
'd': '101100',
'e': '100100',
'f': '111000',
'g': '111100',
'h': '111000',
'i': '011000',
'j': '011100',
'k': '100010',
'l': '110010',
'm': '101010',
'n': '101110',
'o': '100110',
'p': '111010',
'q': '111110',
'r': '111010',
's': '011010',
't': '011110',
'u': '100011',
'v': '110011',
'w': '011101',
'x': '101011',
'y': '101111',
'z': '100111',
}
def text_to_braille(text):
return ''.join(BRAILLE_TABLE.get(char, '') for char in text.lower())
def generate_random_key(length):
return os.urandom(length)
def xor_encrypt_decrypt(data, key):
return bytes([b ^ k for b, k in zip(data, key)])
def main():
original_text = "abc"
print("Исходный текст:", original_text)
###текст в брайля
braille_representation = text_to_braille(original_text)
print("Представление в Брайле:", braille_representation)
###брайль в байты
data = int(braille_representation, 2).to_bytes((len(braille_representation) + 7) // 8, byteorder='big')
###keygen по кол ву символов
key = generate_random_key(len(data))
print("Случайный ключ (hex):", key.hex())
###процесс шифрования
encrypted_data = xor_encrypt_decrypt(data, key)
print("Зашифрованные данные в Брайле (hex):", encrypted_data.hex())
###дешифрация
decrypted_data = xor_encrypt_decrypt(encrypted_data, key)
###оьратно в бинарное значение - декрипт
decrypted_braille = bin(int.from_bytes(decrypted_data, byteorder='big'))[2:].zfill(len(braille_representation))
print("Расшифрованные данные в Брайле:", decrypted_braille)
if __name__ == "__main__":
main()2. Сразу же заодно перейдём к тому, чтобы комбинировать методы:
Python: Скопировать в буфер обмена
Код:
import random
###таблица символов Брайля
BRAILLE_TABLE = {
'A': 0b100000,
'B': 0b110000,
'C': 0b101000,
'D': 0b101100,
'E': 0b100100,
'F': 0b111000,
'G': 0b111100,
'H': 0b110100,
'I': 0b011000,
'J': 0b011100,
'K': 0b100010,
'L': 0b110010,
'M': 0b101010,
'N': 0b101110,
'O': 0b100110,
'P': 0b111010,
'Q': 0b111110,
'R': 0b110110,
'S': 0b011010,
'T': 0b011110,
'U': 0b100011,
'V': 0b110011,
'W': 0b011101,
'X': 0b101011,
'Y': 0b101111,
'Z': 0b100111,
}
###reverse таблица для расшифровки
REVERSE_BRAILLE_TABLE = {v: k for k, v in BRAILLE_TABLE.items()}
def generate_random_key_sequence(length):
return [random.randint(0, 63) for _ in range(length)] ###гсп ключей 6 bit
def xor_operation(cell, key):
return cell ^ key ###применяем XOR к ячейке 6 bit
def shift_bits(cell, shift_amount):
shift_amount %= 6 ###сдвиг битов влево с циклом переноса
return ((cell << shift_amount) & 0b111111) | (cell >> (6 - shift_amount))
def encrypt_message(message, key_sequence):
###шифрование
encrypted_message = []
for i, char in enumerate(message):
if char not in BRAILLE_TABLE:
raise ValueError(f"Символ {char} отсутствует в таблице Брайля.")
cell = BRAILLE_TABLE[char]
key = key_sequence[i % len(key_sequence)]
###функция XOR-операции
cell = xor_operation(cell, key)
###сдвиг на кол-во единиц в ключе
shift_amount = bin(key).count("1")
cell = shift_bits(cell, shift_amount)
encrypted_message.append(cell)
return encrypted_message
def decrypt_message(encrypted_message, key_sequence):
###расшифровка сообщения
decrypted_message = []
for i, cell in enumerate(encrypted_message):
key = key_sequence[i % len(key_sequence)]
###братный сдвиг
shift_amount = bin(key).count("1")
cell = shift_bits(cell, -shift_amount)
###обратный XOR
cell = xor_operation(cell, key)
if cell not in REVERSE_BRAILLE_TABLE:
raise ValueError(f"Неизвестный шифр: {cell}")
decrypted_message.append(REVERSE_BRAILLE_TABLE[cell])
return ''.join(decrypted_message)
###применение к ABC
if __name__ == "__main__":
original_message = "ABC"
key_sequence = generate_random_key_sequence(len(original_message))
print("Исходное сообщение:", original_message)
print("Секретный ключ:", key_sequence)
encrypted = encrypt_message(original_message, key_sequence)
print("Зашифрованное сообщение:", encrypted)
decrypted = decrypt_message(encrypted, key_sequence)
print("Расшифрованное сообщение:", decrypted)Задача стояла не самая простая, для наглядности я не стал вводить и задавать специальные символы и какие-то подобные дполнительные значения, поэтому любой апгрейд на ваше усмотрение будет принят именно как апгрейд, а не критика меня как немного ленивого программиста :t
Подведём итоги.
Что ж, я очень надеюсь, что я смог обоснованно привнести задатки возможной концепции шифрования, веря, что кому-то это будет интересно.
Некоторые хотят иметь собственные методы шифрования и передачи данных, исходя из потребностей, вот и деливери оф креатив с использованием Брайля подъехал. Это лишь одна идея в зародыше из множества возможных, без реализации безопасного обмена ключами. Учитывая, что математика очень важна в самой методологии, некоторые принципы и столпы шифрования требуют гораздо больше знаний в области прикладной математики, вовзведённого аналитического подхода, программно-вычислительных возможностей и мозгов, чем есть у автора. Однако, все комментарии и желания совместных доработок - most welcome!
Всем мира в наступившем году и до новых встреч!